الــــــمـــبـــــدأ الـــــــنـــــظري

الاهتزازات الحرة غير المتخامدة

تعريف

الاهتزازات الحرة غير المخمدة هي تلك الاهتزازات الناتجة عن إزاحة النظام عن وضع توازنه، أو اكتساب إحدى نقاطه المادية سرعة ابتدائية ثم نتركه يهتز بحرية دون أي قوة خارجية.[1]

دراسة نظام ميكانيكي

لتكن الجملة الميكانيكية في الشكل المقابل, نزيح الكتلة عن موضع التوازن بالمقدار..ثم نتركها تهتز بصورة عمودية بدون سرعة ابتدائية, يكون منحى الإراحة بدلالة الزمن على صورة دالة جيبية و التعبير الرياضي لهذه الدالة يعطى بالشكل :

x ( t ) = A cos ( ω t ) ............ ( 1.1 ) x(t) = A cos( %omega t) ............( 1.1 )
الشكل 1.1 : هزاز مروني

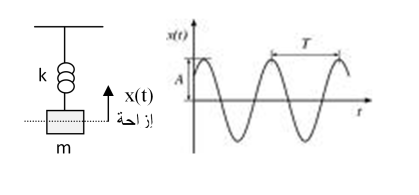
نشتق العبارة مرتين:

d 2 x d t 2 = − ω 2 A cos ( ω t ) { d^{2}x} over {d t^{2}} = - %omega ^{2} A cos( %omega t)
x ¨ ( t ) + ω 2 x ( t ) = 0 .............. ( 1.2 ) ddot x (t) + %omega ^{2} x(t) = 0 ..............( 1.2 )

تمثل المعادلة التفاضلية المعممة لحركة كتلة

الشكل 2.1 : حركة كتلة معلقة بنابض
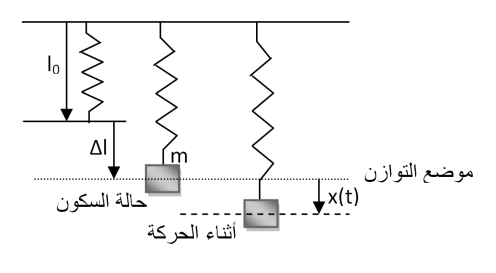
في حالة السكون

نبحث عن ω: نطبق قانون نيوتن الثاني ( مبدأ الأساسي للتحريك)

∑ F ⃗ = 0 ⃗ sum widevec {F} = vec 0

نجد:

mg = K Δ l .................... ( 1.3 ) mg = K %DELTA l ....................(1.3 )
في حالة الحركة

نطبق قانون نيوتن الثاني ( مبدأ الأساسي للتحريك)

∑ F ⃗ = m γ ⃗ sum vec F = m vec %gamma

و منه:

X ¨ ( t ) + K m ⋅ X ( t ) = 0 .............. ( 1.4 ) ddot X(t) + {K} over {m} cdot X(t) = 0 ..............( 1.4 )

و هي تمثل المعادلة التفاضلية لحركة الكتلة الاهتزازية غير المتخامدة (EDM[2]).

بمقارنة المعادلتين (1.2) و (1.4) نجد أن التردد الطبيعي لحركة الكتلة في النظام الميكانيكي هو :

ω 0 2 = K m %omega _{0}^{2} = {K} over {m}

التطبيق على النظام الكهربائي

بتطبيق قانون كيرشوف على الدارة الكهربائية الموافقة للجملة الميكانيكية السابقة.

الشكل 3.1 : الدارة LC

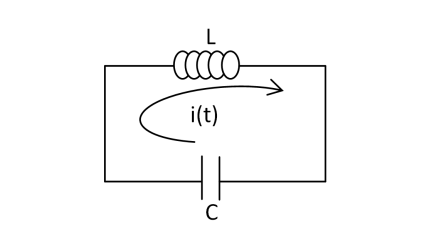
نجد:

V L ( t ) + V C ( t ) = 0 ............. ( 1.5 ) V_{L}(t) + V_{C}(t) = 0 .............( 1.5 )

و منه:

q ¨ + 1 LC ⋅ q = 0 ............ ( 1.6 ) ddot q + {1} over {LC} cdot q = 0 ............( 1.6 )

تمثل معادلة تفاضلية من الدرجة "2" للإهتزازات التوافقية الموافقة للصيغة المعممة (1.2)

بمقارنة المعادلتين (1.2) و (1.6) نجد:

ω 0 2 = 1 LC %omega _{0}^{2} = {1} over {LC}

يمكننا عمل مماثلة بين النظم المهتزة الكهربائية و الميكانيكية كما هو موضح في الجدول الموالي:

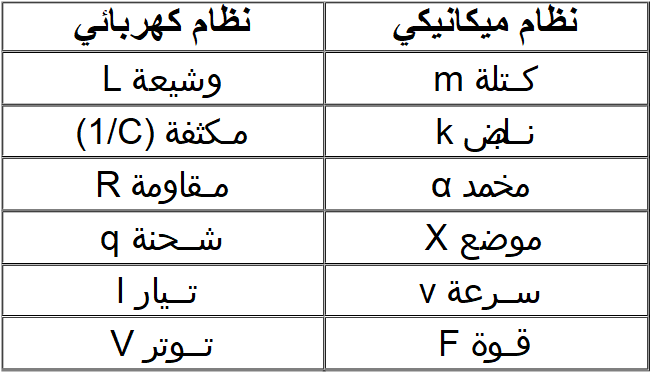
الاهتزازات الحرة المتخامدة ( التخامد اللزوجي)

تعريف

هي تلك الاهتزازات التي تتناقص سعتها مع مرور الزمن حتى تنعدم و ذلك بسبب تبدد طاقتها نتيجة تأثير قوى التخامد أو الاحتكاك عليها[3]. و هناك أنواع من التخامد نذكر منها:

1- التخامد اللزوجي.

2- التخامد الصلب ( تخامد كولومب ).

يعتبر التخامد اللزوجي أكثر الأنواع بساطة في التحليل الرياضي و يتم تمثيل قوة التخامد كدالة للسرعة وفق العلاقة التالية:

F ⃗ = − α X ˙ ⃗ vec F = - %alpha vec dot X

α: يمثل معامل التخامد اللزوجي.

دراسة نظام ميكانيكي

نأخذ نظاما ميكانيكيا متخامد يتكون من كتلة و مخمد و نابض كما في الشكل المقابل:

الشكل 4.1 : هزاز مروني متخامد

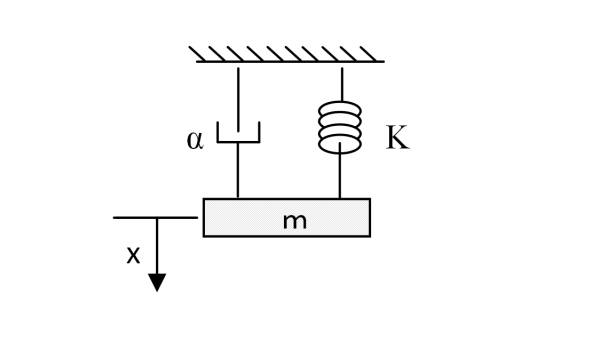
في حالة السكون نجد:

mg = K ⋅ Δ l mg = K cdot %DELTA l

أما في حالة في حالة الحركة فنجد:

X ¨ ( t ) + α m X ˙ ( t ) + K m X ( t ) = 0 .......... ( 1.7 ) ddot X(t) + { %alpha } over {m} dot X(t) + {K} over {m} X(t) = 0 ..........( 1.7 )

و نكتب الشكل العام للمعادلة أعلاه:

X ¨ ( t ) + 2 δ X ˙ ( t ) + ω 0 2 X ( t ) = 0 ............. ( 1.8 ) ddot X(t) + 2 %delta dot X(t) + %omega _{0}^{2}X(t) = 0 .............( 1.8 )

و هي تمثل معادلة تفاضلية من الدرجة "2" لحركة نظام مهتز بصورة حرة متخامدة.

بمقارنة المعادلتين (1.7) و (1.8) نجد معامل التخامد δ و نسبة التخامد ε حيث:

δ = α 2 m %delta = { %alpha } over {2m}
ε = δ ω 0 %varepsilon = { %delta } over { %omega _{0}}

حل هذه المعادلة يتعلق بالمميز:

Δ ´ = δ 2 − ω 0 2 acute %DELTA = %delta ^{2} - %omega _{0}^{2}

-الحالة الأولى:

Δ ` < 0 ⇒ δ < ω 0 grave %DELTA < 0 drarrow %delta < %omega _{0}

في هذه الحالة لدينا جذران مركبان وتكون الإهتزازات متناقصة السعة أي متخامدة و النظام شبه دوري، و حل المعادلة يكون من الشكل :

X ( t ) = C e − δ t ( ω a t + φ ) / ω a = ω 0 2 − δ 2 X(t) = C func e^{ - %delta t } ( %omega _{a} t+ %varphi ) / %omega _{a} = sqrt{ %omega _{0}^{2} - %delta ^{2} }

- الحالة الثانية:

Δ ` ⩾ 0 ⇒ δ ⩾ ω 0 grave %DELTA geslant 0 drarrow %delta geslant %omega _{0}

الجذران حقيقيان و لا يكون الحل جيبي و الحركة غير دورية أي أنّ النظام غير دوري.

- الحالة3:

Δ ` = 0 ⇒ δ = ω 0 grave %DELTA = 0 drarrow %delta = %omega _{0}

تقبل جذر مضاعف و النظام حرج، و حل المعادلة يكون من الشكل :

X ( t ) = ( At + B ) e − δ t X(t) = ( At + B ) func e^{ - %delta t }

تطبيق على النظام الكهربائي

لتكن الدارة في الشكل المقابل :

الشكل 5.1 : الدارة RLC

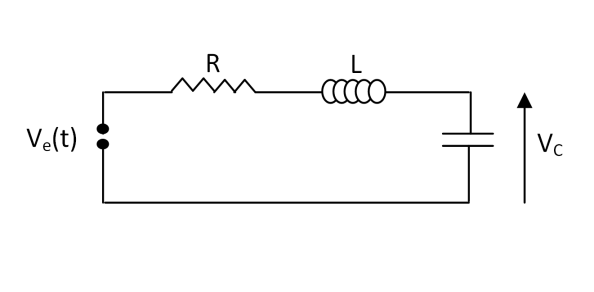
بتطبيق قانون كيرشوف نجد:

V R + V L + V C = 0 ......... ( 1.9 ) V_{R} + V_{L} + V_{C} = 0 .........( 1.9 )

و منه:

q ¨ ( t ) + R L ⋅ q ˙ ( t ) + 1 LC ⋅ q ( t ) = 0 ............ ( 1.10 ) ddot q(t) + {R} over {L} cdot dot q(t) + {1} over {LC} cdot q(t) = 0 ............( 1.10)

و بإعادة كتابة المعادلة وفق المعادلة المعممة (1.8) عندئذ يكتب كل من معامل التخامد و تردد الحركة على الشكل التالي:

δ = 1 2 ⋅ R L ∖ ω 0 = 1 LC %delta = {1} over {2} cdot { {R} over {L} } setminus %omega _{0} = {1} over { sqrt{LC} }

يعتمد حل المعادلة (1.10) على العلاقة بين ω0 و δ أي حسب نوع التخامد و بصورة مماثلة للنموذج الميكانيكي السابق.

التناقص اللــــوغـــارتمي

هي طريقة عملية و بسيطة لإيجاد مقدار التخامد, يُعرّف التناقص اللوغارتمي بأنه اللوغاريتم الطبيعي للنسبة بين سعتين متتاليتين للاهتزازات المتخامدة.

نأخذ كمثال نظام يهتز وفق المعادلة التالية:

X ( t ) = C e − δ t ( ω a t + φ ) / ω a = ω 0 2 − δ 2 X(t) = C func e^{ - %delta t } ( %omega _{a} t+ %varphi ) / %omega _{a} = sqrt{ %omega _{0}^{2} - %delta ^{2} }

كما هو موضح في الشكل الموالي:

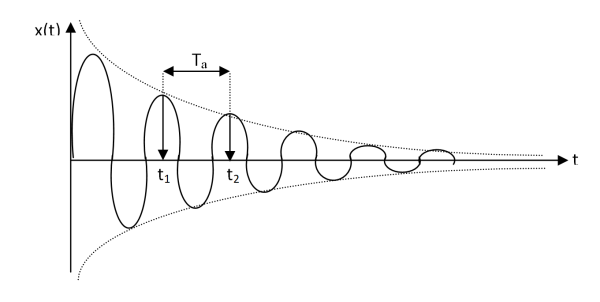
الشكل 6.1 : الشكل البياني للحركة المتخامدة ( حركة شبه دورية )

التناقص اللوغارتمي هو النسبة بين سعتين متتاليتين يفصلهما الزمن الدوري T للذبذبة.

D = ln ( x ( t 1 ) x ( t 2 ) ) = δ t D = ln( {x( t_{1})} over {x( t_{2})} ) = %delta t

و بذلك يمكن إيجاد قيمة نسبة التخامد ξ من خلال التناقص اللوغارتمي:

D = 2 π ζ 1 − ζ 2 = δ t D= {2 %pi %zeta } over { sqrt{ 1 - %zeta ^{2} } } = %delta t